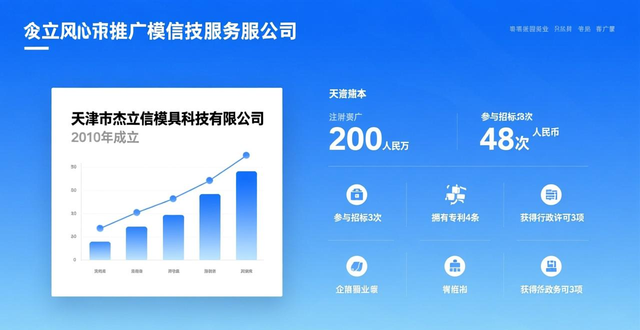
那种关于能够计算机构自由度的方法,有着机构自由度的计算例子,机械原理里机构自由度的计算而言是机构结构分析的关键内容。不管是哪一个机构设计完成之后,所要做的头一件事情便是去计算机构的自由度。机构自由度的计算公式为:F等于3乘以n减去2乘以p再减去p乘以l乘以h。公式这本身是简单的,只需要尽数出活动构件的数量n,低副的数量p,高副的数量p,那么自由度就能够很轻易地计算出来了。利用该公式存在一个前提条件,那即是要先分辨出一些特殊情形,分别是复合铰链,局部自由度以及虚约束,在将这些情形均钻研透彻之后,再运用上述公式进行计算,如此方可获取正确的结果。如下举一个例子,用以说明机构自由度的计算方式。计算图示机构的自由度,并且判定该机构是否具有确定运动。要是存在复合铰链、局部自由度、虚约束,需直接在题图中标注出来。拿到该机构之后,第一步便是寻找到凸轮M,发觉推杆DB尖端存在一个滚子,这个滚子便是局部自由度。几乎永远会出现局部自由度的是滚子推杆的凸轮机构,对于该局部自由度,处理办法是将作为滚子的那个B与BD杆把它们焊接在一起,使之成为一个整体,接着来考察虚约束,虚约束里最常见的情形是某一个构件跟机架之间存在导路重合或者平行的移动副,这里身为FH的构件在F、G、H这三个地方有三个移动副与机架相连接,而这三个移动副的导路是重合的,此时仅有一个起作用,其他的就属于虚约束,对于虚约束,只保留其中的一个,其他的全部去除。最后要考虑的是复合铰链,复合铰链会出现在转动副存在的地方。要是在转动副的位置,有两个以上的构件相互连接,那么这个铰链便是复合铰链。从上面的图能够看出,J点有三个构件相连,分别是IJ、KJ、JL,所以J这里是复合铰链。对于复合铰链,计算转动副数目时,在此处留意就行,要注意这里转动副数目等于相连构件数目减1。综上所述,将局部自由度、虚约束、复合铰链表示出来的结果见下图这般,把滚子B和BD焊接在一起以去掉局部自由度,去掉G、H这两个虚约束,J点有两个转动副。下面进入公式的计算。以下是改写后的句子:活动构件有,齿轮A,齿轮M,连杆IJ,连杆KJ,位于其中的连杆JL,滑块L,焊接了滚子B的连杆BD,连杆DE,连杆FH。总共是9个哦。低副:A,M,I,K,J(2),L(2),C,D,E,F。总共12个。{留意,此处L地方有一个转动副,1个移动副,不可算作复合铰链,说白了铰链乃是转动副,复合表示着多个转动副}高副:齿轮A与齿轮B之间1个,B和凸轮之间1个,总计2个。那么鉴于该机构存在一个原动件,原动件的数量 = 自由度的数量,因而该机构具备确定的运动。下面接着看一个例子。同样,要先对局部自由度进行判断,它常常于凸轮机构之处出现,要是从动件存在滚子,那么滚子即为局部自由度,所以在此处B处属于局部自由度,接着对虚约束加以判断,同样先去查看导路重合的移动副,这里H、I处是杆件HJ与机架之间的两个移动副,其中有一个是虚约束,除此之外,留意在凸轮边上的一个式子,这个式子给出了与铰链K连接的几条线段的几何关系。机构运动简图原本仅应存有图形之举,如果呈现了某些异常的等式,务必要高度警惕不已,这般情形几乎就预示着一种特殊虚约束的现身。由该等式能够察觉,即便不存在LK,滑块M的运动态势并不会产生改变。故而,连杆LK以及转动副L和K皆属于虚约束的范畴,理应予以移除。最终得着重留意复合铰链。它始终会出现在杆件汇聚的转动副所在位置。于图中能够清晰看出,铰链E点相接3根杆件,因此它便是复合铰链。在上述内容综合呈现之后,对于标识好局部自由度、处理完复合铰链以及明确虚约束的机构,其运动简图如下所示。如此一来,将滚子B与BD进行焊接操作,以此方式来处置局部自由度;把移动副H予以去除,同时去掉LK以及铰链L和铰链K,通过这种做法来实现虚约束的消除;而针对E点来讲,在计算时要知晓是2个转动副。接下来着手运用公式去计算自由度情况。其中活动构件包括凸轮A,已焊接滚子B的连杆BD,连杆EC,连杆EF,连杆EG,连杆HJ,连杆JM,滑块M。总计有8个 。低副:A,C,D,E(2),F,G,I,J,M(2),总共计算得出 11 个。高副:在滚子 B 与凸轮 A 之间存在 1 个。那么接下去看最后一个例子。很明显,B 处存在局部自由度;G,H 之中有一个属于虚约束,而且 D 处是复合铰链。标志呈现如下图所示。将滚子 B 和 BC 杆焊接到一起,那么在此处 BD 和 BC 构成一个铰链连接,存在一个转动副;去。